Pentagonal Number Theorem

Pentagonal Number Theorem은 분할수 $p(n)$을 $\mathcal{O}(n^{1.5})$에 구할 수 있게 해주는 멋진 점화식이다.

BOJ 문제는 모르고, Project Euler 78번 으로 연습해볼 수 있다.

koosaga님이 추천해주신 꿀이 뚝뚝 떨어지는 왕기초 연습문제도 Codeforces에 있다.

 

생성함수에 대한 기본적인 지식을 전제한다.

이탤릭체로 표기된 용어는 임의로 지어낸 용어로, 공식적인 용어와 다를 수 있다.

---

분할수와 그 생성함수 

 

 

자연수 $n \ge 0$의 분할수 $p(n)$이란, 합이 $n$이 되는 단조 감소하는 자연수열(분할)의 개수를 말한다.

물론 빈 수열의 합은 0이기 때문에 $p(0) = 1$이다. 엌ㅋㅋㅋㅋㅋ

 

좀 더 정상적인 예시로, $n = 4$에 대해서 조건을 만족하는 분할은 $\{4\},\{3,1\},\{2,2\},\{2,1,1\},\{1,1,1,1\}$로 총 5개이므로 $p(4) = 5$가 된다.

 

그런데 잘 생각해보면, 각각의 분할에 해당하는 집합을 전부 다 쓸 필요 없이 ($i$, $i$의 개수)만 들고 있어도 된다. $n = 4$에 이 예시를 적용하면 $4^{1}, 3^{1}1^{1}, 2^{2}, 2^{1}1^{2}, 1^{4}$와 같이 된다.

 

이를 '다항식'을 이용하여 표현해보자. 즉, $2^{2}$와 같이 표기하던 것을 $(x^{2})^{2}$와 같이 표기를 바꾸면, $n = 4$의 예시는 아래와 같이 바뀐다.

$$(x^4)^1, (x^3)^{1}(x^1)^{1}, (x^2)^2, (x^2)^1(x^1)^2, (x^1)^4$$

 

당연하게도 각각의 항은 모두 $4$차식이기 때문에, 단순히 이들을 더하면 $5x^{4} = p(4)x^{4}$가 된다!

 

$$p(4)x^4 = 5x^4 =(x^4)^1 + (x^3)^{1}(x^1)^{1} + (x^2)^2 + (x^2)^1(x^1)^2 + (x^1)^4$$

 

아하, 뭔가 motivation이 온다. 아무 생각 없이 $1$을 $k_1$개, $2$를 $k_2$개, $t$를 $k_t$개, .... 뽑아서 만든 tuple $(k_1, k_2, \cdots, k_t, \cdots)$은 $k_1 + 2k_2 + \cdots + tk_t + \cdots$의 분할 하나와 정확히 일대일대응이 된다! 

 

여기에 아까의 다항식 formalism을 씌우면, 다음의 생성함수 표현이 그렇게 어색하지 않다.

 

$$\sum_{n=0}^{\infty} p(n)x^{n} = (1+x+x^{2}+\cdots +)(1+x^{2}+(x^{2})^{2} + \cdots + )\cdots(1+x^{t} + (x^{t})^{2} + \cdots + )\cdots$$

 

따라서 $p(n)$의 생성함수는 아래와 같이 나타낼 수 있다.

$$\sum_{n=0}^{\infty} p(n)x^{n} = \prod_{i=1}^{\infty} \frac{1}{1-x^{i}}$$

 

EPNT and its consequences

Theorem EPNT. (Euler's Pentagonal Number Theorem) 다음의 항등식이 성립한다.

 

$$\prod_{i=1}^{\infty} (1-x^{i}) = 1 + \sum_{k=1}^{\infty} (-1)^{k} (x^{k(3k-1)/2} + x^{k(3k+1)/2}) = \sum_{k=-\infty}^{\infty} (-1)^{k} x^{k(3k-1)/2}$$

 

이 때 $g_k = k(3k-1)/2$가 우리가 아는 삼각수, 사각수, 오각수, ...의 오각수에 해당되고, 그래서 Pentagonal Number라고 부른다. $k$에 $-k$를 대입하면 $g_{-k} = k(3k+1)/2$가 나오기 때문에 Theorem의 가장 오른쪽 식을 얻을 수 있다.

 

증명은 잠시 미루고, 이를 이용하여 얻을 수 있는 결과에 먼저 집중하자. 위에서 구한 $p(n)$의 생성함수와 Theorem의 식을 곱하면 1이 나와야 한다. 따라서

 

$$\sum_{n=0}^{\infty}p(n)x^{n} \cdot \left(1 + \sum_{k=1}^{\infty} (-1)^{k} (x^{k(3k-1)/2} + x^{k(3k+1)/2}) \right) = 1$$이 성립한다.

 

따라서 $n \ge 1$에 대해 위 식의 $n$차항을 얻으면 다음의 식이 나온다.

$$p(n) - p(n - g_1) - p(n - g_{-1}) + p(n-g_{2}) + p(n-g_{-2}) + \cdots = 0$$

이항하면,

$$p(n) = p(n-g_1) + p(n-g_{-1}) - p(n-g_2) - p(n-g_{-2}) + p(n-g_3) + p(n-g_{-3}) + \cdots$$

 

저 합은 당연히 $n \ge g_k$인 $k$까지만 계산하면 된다. $g_k$는 $\mathcal{O}(k^{2})$ 스케일이므로, 위 점화식에는 최대 $\mathcal{O}(\sqrt{n})$개의 항만 등장하니 $p(n)$을 $\mathcal{O}(n^{1.5})$ 시간에 구할 수 있다!

 

이 점화식을 이용해서 코딩 문제를 풀고 싶은 거라면 여기까지만 읽으면 된다. 아래는 PE 078번을 해결한 코드이다.

	#include <bits/stdc++.h>
	using namespace std;
	using ll = long long;
	const int mod = 1e6;
	vector<int> p({1});
	vector<int> g;
	int k=1, kc;
	int main(){
	for(int n = 1;;n++){
	p.push_back(0);
	int &q = p.back();
	if(kc){
	if(ll(k) * (3*k+1) == 2ll*n){
	g.push_back(ll(k) * (3*k+1)/2);
	kc = 0;
	++k;
	}
	}else{
	if(ll(k) * (3*k-1) == 2ll*n){
	g.push_back(ll(k) * (3*k-1)/2);
	kc = 1;
	}
	}
	for(int i = 0; i < g.size(); i++){
	if((i&3) < 2){
	q = (q + p[n-g[i]])%mod;
	}else{
	q = (q + mod - p[n-g[i]])%mod;
	}
	}
	if(n <= 10) cout << n << ' ' << q << '\n';
	if(q == 0){
	cout << n << "\n";
	break;
	}
	}
	}

view raw ProjectEuler 78.cpp hosted with ❤ by GitHub

 

 

Proof of EPNT - introduction

$p(n)$의 생성함수를 구할 때는 분할수의 조합적 의미로부터 생성함수를 얻었지만, 이번엔 거꾸로 Theorem의 생성함수에서 분할같은 의미를 얻어내 보자.

 

다음의 strict한 분할수 $q(n)$을 생각해보자.

$q(n)$ : 합이 $n$이 되는 강감소하는 자연수열(strict한 분할)의 개수. ($q(4) = 2$가 된다)

 

$q(n)$의 생성함수를 생각해보면, 각각의 (strict한) 분할에서 한 수는 최대 한 번만 사용될 수 있으므로 $q(n)$의 생성함수는 Theorem의 각 항에서 부호를 뺀 $(1+x^{i})$의 무한곱과 같게 된다.

 

$$\sum_{n=0}^{\infty} q(n)x^{n} = \prod_{i=1}^{\infty} (1+x^{i})$$

 

위 식의 우변에 부호를 붙이면; 즉 $x^i$를 $-x^i$로 고치면 무슨 일이 일어날까? $q(4)$의 예시를 생각해보면,

 

$4$의 strict한 분할 중 하나인 $\{4\}$는 $x^{4}$였다가 $-x^{4}$로 바뀐다.

$4$의 또다른 strict한 분할인 $\{3,1\}$은 $x^{3}x^{1}$이었다가 $(-x^3)(-x^1) = x^{4}$로 바뀐다.

 

즉, $n$의 strict한 분할 중 항이 짝수 개인 것에는 +부호가, 홀수 개인 것에는 -부호가 붙게 됨을 알 수 있다. 따라서,

 

$q_{even}(n)$ : 합이 $n$이 되는 강감소하는 길이가 짝수인 자연수열(strict한 짝분할)의 개수.

$q_{odd}(n)$ : 합이 $n$이 되는 강감소하는 길이가 홀수인 자연수열(strict한 홀분할)의 개수.

 

$$\sum_{n=0}^{\infty} (q_{even}(n) - q_{odd}(n))x^{n} = \prod_{i=1}^{\infty} (1-x^{i})$$

의 relation이 성립하게 되고, 우리가 증명해야 할 명제는 다음과 같다.

 

Claim.

 

$$q_{even}(n) - q_{odd}(n) = \begin{cases} (-1)^{k} & (n = k(3k\pm1)/2) \\ 0 & (\text{otherwise}) \end{cases}$$

 

우리는 이제야 무엇을 증명해야 할 지 알았다.

 

Proof of EPNT - Involution

Claim을 증명하기 위해 involution을 잡으려고 한다. 이름이 생소해서 그렇지 그다지 어렵지 않은 trick이다.

어떤 strict한 짝분할 $Q$에, 모든 strict한 분할에 대해 잘 정의된 변환 $\lambda$를 씌워 strict한 홀분할 $Q^{*} = \lambda(Q)$를 만든다. 이 때 다시 $\lambda^{2}(Q) = \lambda(Q^{*}) = Q$가 되도록 $\lambda$를 잘 잡을 수 있으면 이러한 $\lambda$를 involution이라고 한다. 즉, 좀 더 강한 bijection에 지나지 않는다.

 

25 = 8 + 7 + 6 + 4의 Ferrer diagram.

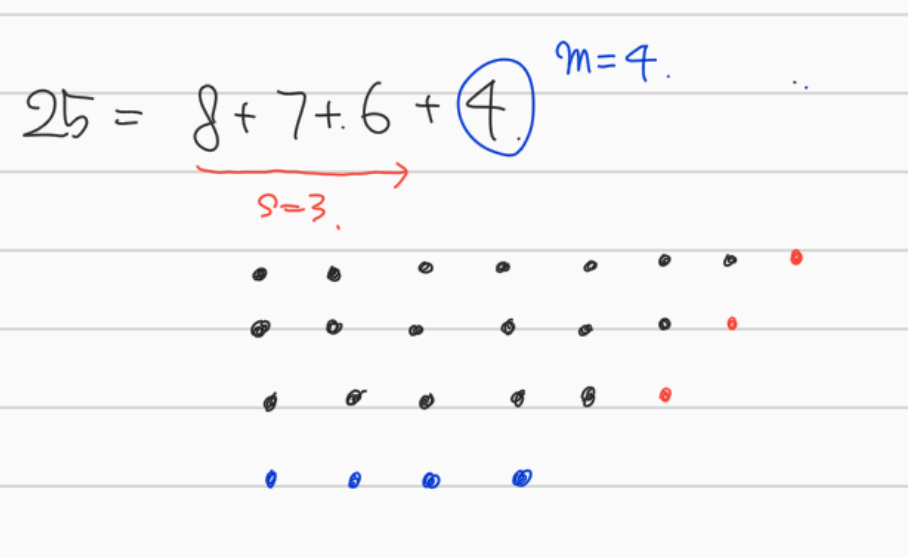
Partition과 관련한 대응을 생각할 때는 위와 같은 Ferrer diagram을 생각하는 게 도움이 된다. 25 = 8 + 7 + 6 + 4의 strict한 분할을 위 그림과 같이 나타낸 걸 Ferrer diagram이라고 한다. 즉 $n = q_1 + q_2 + \cdots + q_k$에서, 맨 위 row에 $q_1$개, 그 아래에 $q_2$개, ... 맨 아래 row에 $q_k$개의 점을 나열한 것이다.

 

이제 involution $\lambda$를 잡아보자. 이를 결정하는 인자는 bottom row의 개수; 분할에서 가장 작은 값 $m = q_k$와,

오른쪽 위 끝점에서 그은 y = x와 평행한 직선 위의 점 개수; $q_s + s - 1 = q_1$을 만족하는 maximal $s$를 비교하자. 위 그림에서 빨간 점의 개수가 $s$, 파란 점의 개수가 $m$이다.

 

 

만약 $m > s$라면, 빨간 점들을 모두 모아 bottom row에 붙이면 된다. 새로 만든 분할은 여전히 strict한 분할이고, row의 개수는 1개 늘어났으므로 그 기우성이 바뀌었다.

 

첫 번째 변환

 

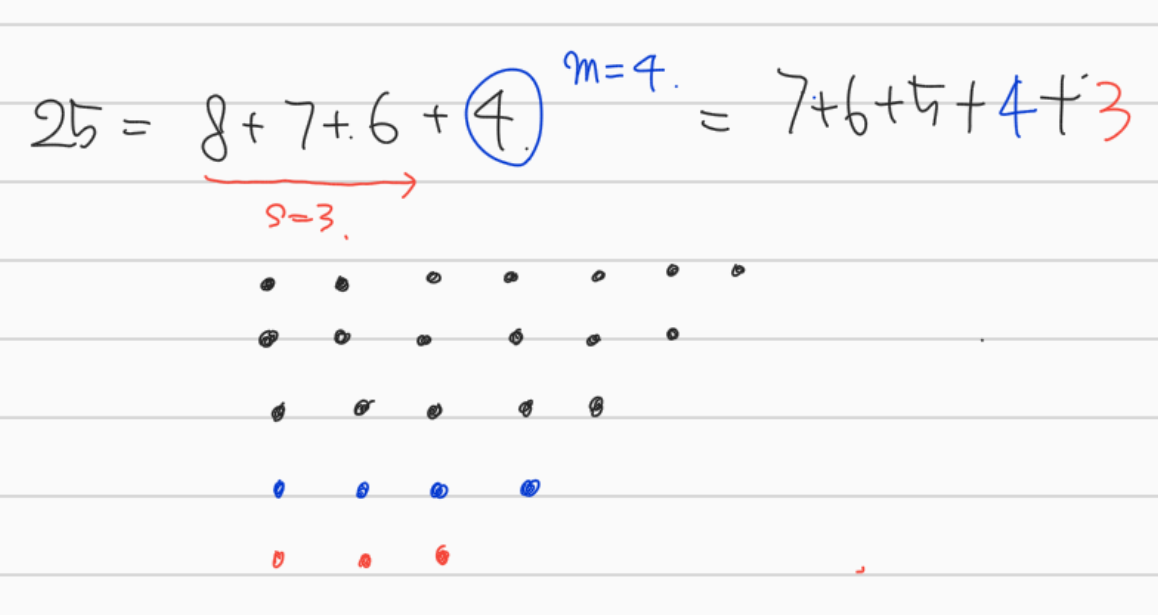
만약 $m \le s$라면, 반대로 bottom row를 떼어서 맨 위부터 대각선을 따라 붙여주면 된다.

 

위 그림의 역변환

어? 그런데, 이 그림에서 맨 아래줄의 '보라색' 점은 bottom row(파란색)에도 해당되고, 대각선(빨간색) 점에도 해당되는 것 같다. 그렇다면 $m$과 $s$의 값에 따라서 $\lambda$가 잘 정의되지 않는 경우가 생기지 않을까?

 

실제로 그러한 경우가 단 2개 발생하고, 그것이 $(-1)^{k}$만큼의 차이를 만든다.

 

1) 보라색 점이 존재하고 (i.e. 수열의 항 개수 $k = s$), $m = s + 1$

15 = 6 + 5 + 4

이 경우 빨간색(+보라색) 점들을 들어 bottom row에 놓으면, bottom row가 15 = 5 + 4 + 3 + 3이 되어 strict한 분할이 아니게 된다. 따라서 이러한 $n$에 대해서는 $s$가 홀수라면 홀분할이, $s$가 짝수라면 짝분할이 1개 더 많게 된다. 이런 경우가 발생할 수 있는 $n$은 $\displaystyle n = m + (m+1) + \cdots + (m+s-1) = (s+1) + \cdots + 2s = \frac{s(3s+1)}{2}$가 된다. 우리는 (짝분할 개수)-(홀분할 개수)를 셀 것이기 때문에 가중치는 $(-1)^s = (-1)^k$이다.

 

2) 보라색 점이 존재하고, $m = s$

12 = 5 + 4 + 3

위 그림의 경우 파란색(+보라색) 점을 들어내는 순간 row가 2개밖에 남지 않아서 대각선상에 점을 배치할 수가 없게 된다. 따라서 $s$가 홀수라면 홀분할이, 짝수라면 짝분할이 1개 더 많게 되고, 가능한 $n$은 $n = s(3s-1)/2$가 된다. 1)의 경우와 동일하게 가중치는 $(-1)^{s}$가 된다.

 

이러한 2가지 예외를 제외하고는 strict한 짝분할, 홀분할은 involution에 의한 일대일대응을 이루게 되고, 따라서 Claim을 증명할 수 있다. $\blacksquare$