2019. 9. 16. 07:00ㆍ수학 이론/이산수학
Pentagonal Number Theorem은 분할수 \(p(n)\)을 \(\mathcal{O}(n^{1.5})\)에 구할 수 있게 해주는 멋진 점화식이다.
BOJ 문제는 모르고, Project Euler 78번 으로 연습해볼 수 있다.
koosaga님이 추천해주신 꿀이 뚝뚝 떨어지는 왕기초 연습문제도 Codeforces에 있다.
생성함수에 대한 기본적인 지식을 전제한다.
이탤릭체로 표기된 용어는 임의로 지어낸 용어로, 공식적인 용어와 다를 수 있다.
분할수와 그 생성함수
자연수 \(n \ge 0\)의 분할수 \(p(n)\)이란, 합이 \(n\)이 되는 단조 감소하는 자연수열(분할)의 개수를 말한다.
물론 빈 수열의 합은 0이기 때문에 \(p(0) = 1\)이다. 엌ㅋㅋㅋㅋㅋ
좀 더 정상적인 예시로, \(n = 4\)에 대해서 조건을 만족하는 분할은 \(\{4\},\{3,1\},\{2,2\},\{2,1,1\},\{1,1,1,1\}\)로 총 5개이므로 \(p(4) = 5\)가 된다.
그런데 잘 생각해보면, 각각의 분할에 해당하는 집합을 전부 다 쓸 필요 없이 (\(i\), \(i\)의 개수)만 들고 있어도 된다. \(n = 4\)에 이 예시를 적용하면 \(4^{1}, 3^{1}1^{1}, 2^{2}, 2^{1}1^{2}, 1^{4}\)와 같이 된다.
이를 '다항식'을 이용하여 표현해보자. 즉, \(2^{2}\)와 같이 표기하던 것을 \((x^{2})^{2}\)와 같이 표기를 바꾸면, \(n = 4\)의 예시는 아래와 같이 바뀐다.
$$ (x^4)^1, (x^3)^{1}(x^1)^{1}, (x^2)^2, (x^2)^1(x^1)^2, (x^1)^4$$
당연하게도 각각의 항은 모두 \(4\)차식이기 때문에, 단순히 이들을 더하면 \(5x^{4} = p(4)x^{4}\)가 된다!
$$ p(4)x^4 = 5x^4 =(x^4)^1 + (x^3)^{1}(x^1)^{1} + (x^2)^2 + (x^2)^1(x^1)^2 + (x^1)^4 $$
아하, 뭔가 motivation이 온다. 아무 생각 없이 \(1\)을 \(k_1\)개, \(2\)를 \(k_2\)개, \(t\)를 \(k_t\)개, .... 뽑아서 만든 tuple \((k_1, k_2, \cdots, k_t, \cdots)\)은 \(k_1 + 2k_2 + \cdots + tk_t + \cdots\)의 분할 하나와 정확히 일대일대응이 된다!
여기에 아까의 다항식 formalism을 씌우면, 다음의 생성함수 표현이 그렇게 어색하지 않다.
$$ \sum_{n=0}^{\infty} p(n)x^{n} = (1+x+x^{2}+\cdots +)(1+x^{2}+(x^{2})^{2} + \cdots + )\cdots(1+x^{t} + (x^{t})^{2} + \cdots + )\cdots $$
따라서 \(p(n)\)의 생성함수는 아래와 같이 나타낼 수 있다.
$$ \sum_{n=0}^{\infty} p(n)x^{n} = \prod_{i=1}^{\infty} \frac{1}{1-x^{i}} $$
EPNT and its consequences
Theorem EPNT. (Euler's Pentagonal Number Theorem) 다음의 항등식이 성립한다.
$$ \prod_{i=1}^{\infty} (1-x^{i}) = 1 + \sum_{k=1}^{\infty} (-1)^{k} (x^{k(3k-1)/2} + x^{k(3k+1)/2}) = \sum_{k=-\infty}^{\infty} (-1)^{k} x^{k(3k-1)/2}$$
이 때 \(g_k = k(3k-1)/2\)가 우리가 아는 삼각수, 사각수, 오각수, ...의 오각수에 해당되고, 그래서 Pentagonal Number라고 부른다. \(k\)에 \(-k\)를 대입하면 \(g_{-k} = k(3k+1)/2\)가 나오기 때문에 Theorem의 가장 오른쪽 식을 얻을 수 있다.
증명은 잠시 미루고, 이를 이용하여 얻을 수 있는 결과에 먼저 집중하자. 위에서 구한 \(p(n)\)의 생성함수와 Theorem의 식을 곱하면 1이 나와야 한다. 따라서
$$ \sum_{n=0}^{\infty}p(n)x^{n} \cdot \left(1 + \sum_{k=1}^{\infty} (-1)^{k} (x^{k(3k-1)/2} + x^{k(3k+1)/2}) \right) = 1$$이 성립한다.
따라서 \(n \ge 1\)에 대해 위 식의 \(n\)차항을 얻으면 다음의 식이 나온다.
$$p(n) - p(n - g_1) - p(n - g_{-1}) + p(n-g_{2}) + p(n-g_{-2}) + \cdots = 0$$
이항하면,
$$p(n) = p(n-g_1) + p(n-g_{-1}) - p(n-g_2) - p(n-g_{-2}) + p(n-g_3) + p(n-g_{-3}) + \cdots $$
저 합은 당연히 \(n \ge g_k\)인 \(k\)까지만 계산하면 된다. \(g_k\)는 \(\mathcal{O}(k^{2})\) 스케일이므로, 위 점화식에는 최대 \(\mathcal{O}(\sqrt{n})\)개의 항만 등장하니 \(p(n)\)을 \(\mathcal{O}(n^{1.5})\) 시간에 구할 수 있다!
이 점화식을 이용해서 코딩 문제를 풀고 싶은 거라면 여기까지만 읽으면 된다. 아래는 PE 078번을 해결한 코드이다.
Proof of EPNT - introduction
\(p(n)\)의 생성함수를 구할 때는 분할수의 조합적 의미로부터 생성함수를 얻었지만, 이번엔 거꾸로 Theorem의 생성함수에서 분할같은 의미를 얻어내 보자.
다음의 strict한 분할수 \(q(n)\)을 생각해보자.
\(q(n)\) : 합이 \(n\)이 되는 강감소하는 자연수열(strict한 분할)의 개수. (\(q(4) = 2\)가 된다)
\(q(n)\)의 생성함수를 생각해보면, 각각의 (strict한) 분할에서 한 수는 최대 한 번만 사용될 수 있으므로 \(q(n)\)의 생성함수는 Theorem의 각 항에서 부호를 뺀 \((1+x^{i})\)의 무한곱과 같게 된다.
$$ \sum_{n=0}^{\infty} q(n)x^{n} = \prod_{i=1}^{\infty} (1+x^{i}) $$
위 식의 우변에 부호를 붙이면; 즉 \(x^i\)를 \(-x^i\)로 고치면 무슨 일이 일어날까? \(q(4)\)의 예시를 생각해보면,
\(4\)의 strict한 분할 중 하나인 \(\{4\}\)는 \(x^{4}\)였다가 \(-x^{4}\)로 바뀐다.
\(4\)의 또다른 strict한 분할인 \(\{3,1\}\)은 \(x^{3}x^{1}\)이었다가 \((-x^3)(-x^1) = x^{4}\)로 바뀐다.
즉, \(n\)의 strict한 분할 중 항이 짝수 개인 것에는 +부호가, 홀수 개인 것에는 -부호가 붙게 됨을 알 수 있다. 따라서,
\(q_{even}(n)\) : 합이 \(n\)이 되는 강감소하는 길이가 짝수인 자연수열(strict한 짝분할)의 개수.
\(q_{odd}(n)\) : 합이 \(n\)이 되는 강감소하는 길이가 홀수인 자연수열(strict한 홀분할)의 개수.
$$ \sum_{n=0}^{\infty} (q_{even}(n) - q_{odd}(n))x^{n} = \prod_{i=1}^{\infty} (1-x^{i}) $$
의 relation이 성립하게 되고, 우리가 증명해야 할 명제는 다음과 같다.
Claim.
$$ q_{even}(n) - q_{odd}(n) = \begin{cases} (-1)^{k} & (n = k(3k\pm1)/2) \\ 0 & (\text{otherwise}) \end{cases} $$
우리는 이제야 무엇을 증명해야 할 지 알았다.
Proof of EPNT - Involution
Claim을 증명하기 위해 involution을 잡으려고 한다. 이름이 생소해서 그렇지 그다지 어렵지 않은 trick이다.
어떤 strict한 짝분할 \(Q\)에, 모든 strict한 분할에 대해 잘 정의된 변환 \(\lambda\)를 씌워 strict한 홀분할 \(Q^{*} = \lambda(Q)\)를 만든다. 이 때 다시 \(\lambda^{2}(Q) = \lambda(Q^{*}) = Q\)가 되도록 \(\lambda\)를 잘 잡을 수 있으면 이러한 \(\lambda\)를 involution이라고 한다. 즉, 좀 더 강한 bijection에 지나지 않는다.

Partition과 관련한 대응을 생각할 때는 위와 같은 Ferrer diagram을 생각하는 게 도움이 된다. 25 = 8 + 7 + 6 + 4의 strict한 분할을 위 그림과 같이 나타낸 걸 Ferrer diagram이라고 한다. 즉 \(n = q_1 + q_2 + \cdots + q_k\)에서, 맨 위 row에 \(q_1\)개, 그 아래에 \(q_2\)개, ... 맨 아래 row에 \(q_k\)개의 점을 나열한 것이다.
이제 involution \(\lambda\)를 잡아보자. 이를 결정하는 인자는 bottom row의 개수; 분할에서 가장 작은 값 \(m = q_k\)와,
오른쪽 위 끝점에서 그은 y = x와 평행한 직선 위의 점 개수; \(q_s + s - 1 = q_1\)을 만족하는 maximal \(s\)를 비교하자. 위 그림에서 빨간 점의 개수가 \(s\), 파란 점의 개수가 \(m\)이다.
만약 \(m > s\)라면, 빨간 점들을 모두 모아 bottom row에 붙이면 된다. 새로 만든 분할은 여전히 strict한 분할이고, row의 개수는 1개 늘어났으므로 그 기우성이 바뀌었다.
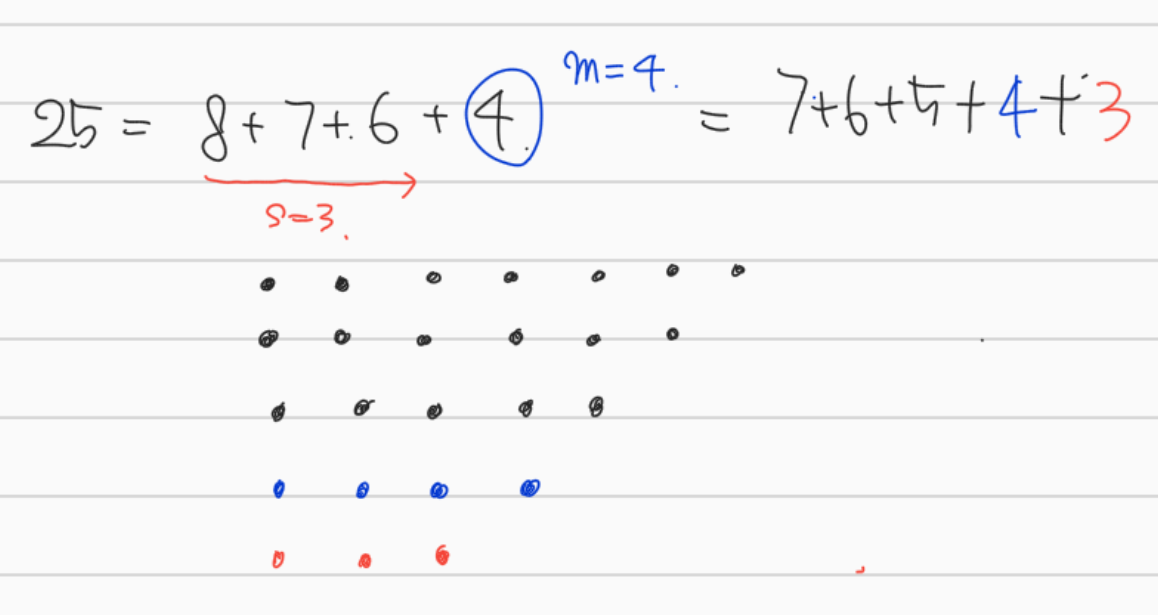
만약 \(m \le s\)라면, 반대로 bottom row를 떼어서 맨 위부터 대각선을 따라 붙여주면 된다.
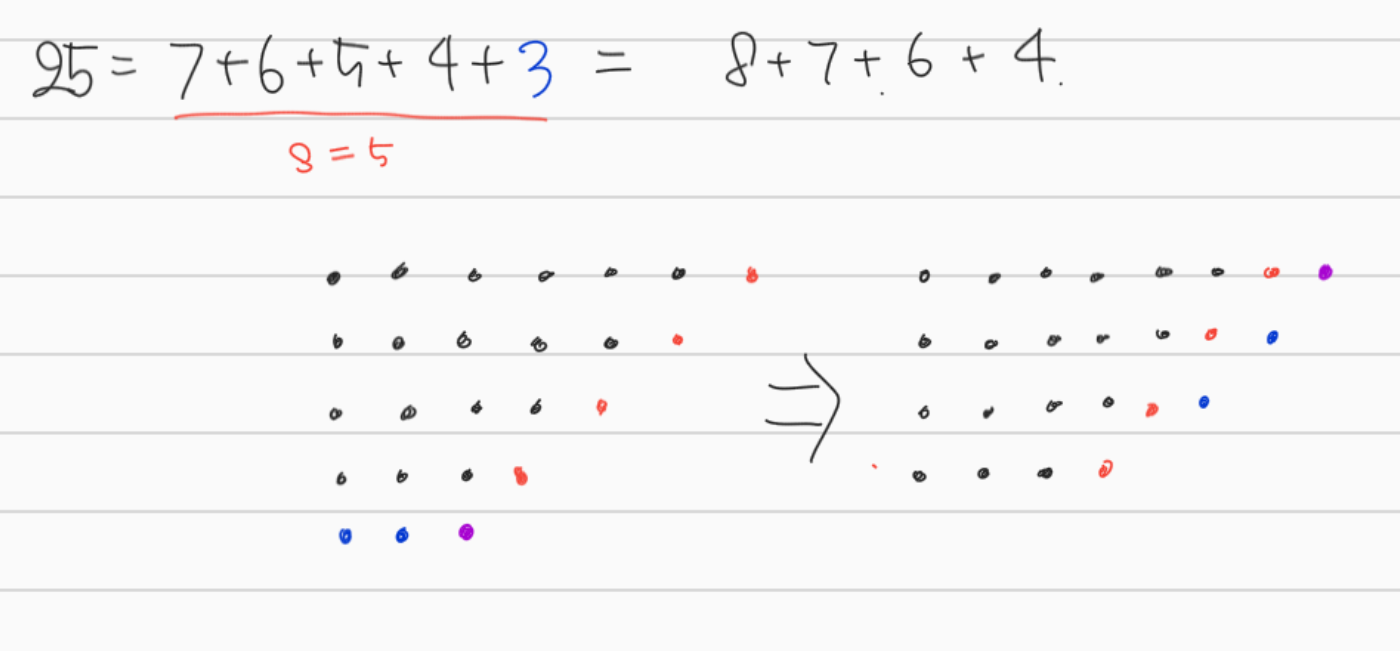
어? 그런데, 이 그림에서 맨 아래줄의 '보라색' 점은 bottom row(파란색)에도 해당되고, 대각선(빨간색) 점에도 해당되는 것 같다. 그렇다면 \(m\)과 \(s\)의 값에 따라서 \(\lambda\)가 잘 정의되지 않는 경우가 생기지 않을까?
실제로 그러한 경우가 단 2개 발생하고, 그것이 \((-1)^{k}\)만큼의 차이를 만든다.
1) 보라색 점이 존재하고 (i.e. 수열의 항 개수 \(k = s\)), \(m = s + 1\)

이 경우 빨간색(+보라색) 점들을 들어 bottom row에 놓으면, bottom row가 15 = 5 + 4 + 3 + 3이 되어 strict한 분할이 아니게 된다. 따라서 이러한 \(n\)에 대해서는 \(s\)가 홀수라면 홀분할이, \(s\)가 짝수라면 짝분할이 1개 더 많게 된다. 이런 경우가 발생할 수 있는 \(n\)은 \(\displaystyle n = m + (m+1) + \cdots + (m+s-1) = (s+1) + \cdots + 2s = \frac{s(3s+1)}{2}\)가 된다. 우리는 (짝분할 개수)-(홀분할 개수)를 셀 것이기 때문에 가중치는 \((-1)^s = (-1)^k\)이다.
2) 보라색 점이 존재하고, \(m = s\)

위 그림의 경우 파란색(+보라색) 점을 들어내는 순간 row가 2개밖에 남지 않아서 대각선상에 점을 배치할 수가 없게 된다. 따라서 \(s\)가 홀수라면 홀분할이, 짝수라면 짝분할이 1개 더 많게 되고, 가능한 \(n\)은 \(n = s(3s-1)/2\)가 된다. 1)의 경우와 동일하게 가중치는 \((-1)^{s}\)가 된다.
이러한 2가지 예외를 제외하고는 strict한 짝분할, 홀분할은 involution에 의한 일대일대응을 이루게 되고, 따라서 Claim을 증명할 수 있다. \(\blacksquare\)
'수학 이론 > 이산수학' 카테고리의 다른 글
| Cayley's theorem in Combinatorics (4) | 2019.12.11 |
|---|---|
| 스털링 수와 다항식 기저 변환 (2) | 2019.09.17 |
| Ore's theorem & Palmer's algorithm (2) | 2019.08.17 |
| Bessel's Correction (Revised) (3) | 2019.03.27 |
| Mirsky's theorem (3) | 2018.11.04 |